1514. Истина, спрятанная в рекуррентности

Рекурсивная функция задана следующим образом:

f(0, 0) = 1,

f(n, r) = , если n > 0 и 0 £ r £ n(k – 1) + 1,

f(n, r) = 0 иначе.

Вычислить значение x = mod m, где m = 10^t.

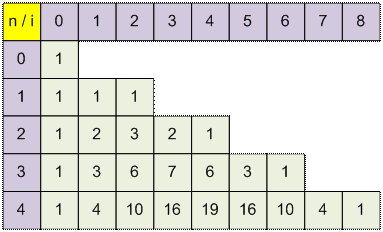
Например, значения f(n, i) при k = 3 имеют вид (в пустых клетках стоят нули):

Вход. Каждая строка содержит три целых числа: k (0 < k < 10¹⁹), n (0 < n < 10¹⁹) и t (0 < t < 10). Последняя строка содержит три нуля и не обрабатывается.

Выход. Для каждого теста в отдельной строке вывести номер теста и значение x. Формат вывода приведен в примере.

Пример входа	Пример выхода
1234 1234 4 2323 99999999999 8 4 99999 9 888 888 8 0 0 0	Case #1: 736 Case #2: 39087387 Case #3: 494777344 Case #4: 91255296

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Рассмотрим все n - цифровые числа в системе исчисления с основанием k (включая числа с ведущими нулями). Общее их количество равно kⁿ. Пусть f(n, r) – количество таких чисел, сумма цифр которых равна r. Тогда

f(n, r) = f(n – 1, r) + f(n – 1, r – 1) + … + f(n – 1, r – k + 1) = .

Минимальная сумма цифр для таких чисел равна 0, максимальная (k – 1) * n. Просуммировав значения f(n, r) для r от 0 до (k – 1) * n, получим общее количество n - цифровых чисел в системе исчисления с основанием k, то есть kⁿ.

Таким образом x = kⁿ (mod 10^t). Поскольку t < 10, то при вычислении модулярной экспоненты достаточно использовать беззнаковый 64-битный целочисленный тип.

Пример

Для первого теста имеет место равенство: 1234¹²³⁴ (mod 10⁴) = 736.

Реализация алгоритма

При вычислении используем беззнаковый 64-битовый целый тип unsigned long long.

Функция вычисления kⁿ mod m с оценкой сложности O(log₂n):

unsigned long long PowMod(unsigned long long x,

unsigned long long y, unsigned long long n)

{

if (!y) return 1;

if (y & 1) return (x * PowMod((x * x) % n, y / 2, n)) % n;

return PowMod((x * x) % n, y / 2, n);

}

Читаем входные значения k, n, t, вычисляем m = 10^t. Находим x = kⁿ (mod 10^t) = (k mod m)ⁿ (mod 10^t). Поскольку k < 10¹⁹, то во избежание переполнения перед вызовом функции powmod следует найти остаток от деления k на m. Таким образом значение первого аргумента k функции powmod будет не более 10⁹ и при вычислении k * k не будет переполнения. Выводим результат с номером теста cs.

int cs = 1;

while(scanf("%llu %llu %llu",&k, &n, &t), k + n + t)

{

m = 1; for(i = 0; i < t; i++) m *= 10;

res = powmod(k % m,n,m);

printf("Case #%d: %lld\n",cs++,res);

}